Weightage: 6 – 7 marks
Get Download Link on your Phone
India’s Most Loved Science & Maths Videos – Packed in a Mobile App!
Introducing Avanti Gurukul App
Concepts covered:
- Probability of an event
- Types of events
- Elementary events
- Sure Event
- Impossible Event
- Complementary events
Expected questions:
- Questions based on finding probability of occurrence of events on the basis of given information are asked for 3 – 4 marks.
Synopsis:
- Probability of an event:
where we assume that the outcomes of the experiment are equally likely, i.e., all the outcomes occur with equal probability.
- Types of events: An event having only one outcome is called an elementary event.
- The sum of the probability of all the elementary events of an experiment will always be equal to 1.Lets say we have a bag with 3 balls identical in shape & size having different colours, say red, blue & green.In this case event of pulling out a red ball is an event having only 1 outcome.Similarly, pulling out a green ball or a blue ball also has one outcome. These events will be called elementary events.Now, in this bag if we add 3 identical yellow balls : Y1, Y2 & Y3Then, pulling out a yellow ball will be an event but pulling out Y1, Y2 & Y3 will be elementary event.In both cases you can see that sum of the probabilities of all the elementary events of an experiment is 1.
- Sure event: When an event is certain to occur, it is called sure event.
- Over here, whenever we put hand in the bag , we will always pull out a ball.Probability of taking out a ball from the bag is 1. Such events are called sure events.
- Impossible event: Events which will never occur are called impossible events. For example, in the above given experiment, if we want to take out a black ball, the probability will be zero.The probability of an event can never be negative and it always lies between
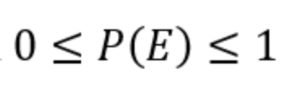
- Complement of an event:
